Un numero intero (pronunciato IN-tuh-jer) è un numero intero (non un numero frazionario) che può essere positivo, negativo o zero.
Esempi di numeri interi sono: -5, 1, 5, 8, 97 e 3,043.
Esempi di numeri che non sono numeri interi sono: -1.43, 1 3/4, 3.14, 09 e 5,643.1.
L'insieme di numeri interi, indicato Z, è formalmente definito come segue:
Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}
Nelle equazioni matematiche, i numeri interi sconosciuti o non specificati sono rappresentati da lettere minuscole in corsivo dalla "tarda metà" dell'alfabeto. I più comuni sono p, q, r e s.
Il set Z è un insieme numerabile. La numerabilità si riferisce al fatto che, anche se potrebbe esserci un numero infinito di elementi in un insieme, quegli elementi possono essere denotati da un elenco che implica l'identità di ogni elemento nell'insieme. Ad esempio, è intuitivo dall'elenco {..., -3, -2, -1, 0, 1, 2, 3, ...} che 356,804,251 e -67,332 sono numeri interi, ma 356,804,251.5, -67,332.89, - 4/3 e 0.232323 ... non lo sono.
Gli elementi di Z può essere accoppiato uno a uno con gli elementi di N, l'insieme dei numeri naturali, senza che nessun elemento venga escluso da nessuno dei due. Permettere N = {1, 2, 3, ...}. Quindi l'accoppiamento può procedere in questo modo:
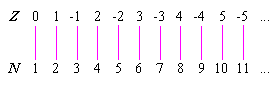
Negli insiemi infiniti, l'esistenza di una corrispondenza uno-a-uno è la cartina di tornasole per determinare la cardinalità, o dimensione. L'insieme dei numeri naturali e l'insieme dei numeri razionali hanno la stessa cardinalità di Z. Tuttavia, gli insiemi di numeri reali, numeri immaginari e numeri complessi hanno una cardinalità maggiore di quella di Z.
