Un numero razionale è un numero determinato dal rapporto tra un numero intero p e un numero naturale q diverso da zero. L'insieme dei numeri razionali è indicato Q, e rappresenta l'insieme di tutti i possibili rapporti tra numeri interi e numeri naturali p / q. Nelle espressioni matematiche, i numeri razionali sconosciuti o non specificati sono rappresentati da lettere minuscole in corsivo dalla fine della metà o dalla fine dell'alfabeto, in particolare r, s , et, e occasionalmente da u a z. I numeri razionali interessano principalmente i teorici. La matematica teorica ha applicazioni potenzialmente di vasta portata nelle comunicazioni e nell'informatica, in particolare nella crittografia e sicurezza dei dati.
Se r e t sono numeri razionali tali che r <t, allora esiste un numero razionale s tale che r <s <t. Questo è vero non importa quanto piccola sia la differenza tra r e t, purché i due non siano uguali. In questo senso, l'insieme Q è "denso". Tuttavia, Q è un insieme numerabile. La numerabilità si riferisce al fatto che, anche se un insieme potrebbe contenere un numero infinito di elementi, e anche se questi elementi potrebbero essere "densamente impaccati", gli elementi possono essere definiti da un elenco che assegna a ciascuno un unico numero in una sequenza corrispondente all'insieme dei numeri naturali N = {1, 2, 3, ...} ..
Per l'insieme dei numeri naturali N e l'insieme dei numeri interi Z, nessuno dei quali è "denso", gli elenchi di denominazione sono semplici Q, è meno ovvio come un tale elenco potrebbe essere costruito. Un esempio appare di seguito. La matrice include tutti i possibili numeri della forma p / q, dove p è un numero intero e q è un numero naturale diverso da zero. Ogni numero razionale possibile è rappresentato nella matrice. Seguendo la linea rosa, pensa a 0 come "prima fermata", 1/1 come "seconda fermata", -1/1 come "terza fermata", 1/2 come "quarta fermata", e così via. Questo definisce un elenco sequenziale (sebbene ridondante) dei numeri razionali. Esiste una corrispondenza uno a uno tra gli elementi della matrice e l'insieme dei numeri naturali N.
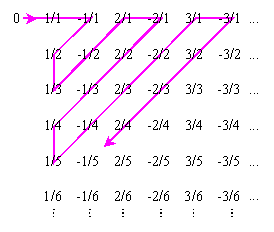
Per dimostrare una vera corrispondenza uno-a-uno tra Q e N, è necessario aggiungere una modifica all'algoritmo mostrato in figura.Alcuni degli elementi nella matrice sono ripetizioni di valori numerici precedenti, ad esempio 2/4 = 3/6 = 4/8 = 5/10, e così via .Queste ridondanze possono essere eliminate imponendo il vincolo "Se un numero rappresenta un valore incontrato in precedenza, saltatelo". In questo modo, si può rigorosamente dimostrare che l'insieme Q ha esattamente lo stesso numero di elementi dell'insieme NAlcune persone lo trovano difficile da credere, ma la logica è valida.
In contrasto con i numeri naturali, interi e razionali, gli insiemi di numeri irrazionali, numeri reali, numeri immaginari e numeri complessi non sono numerabili. Hanno una cardinalità maggiore di quella dell'insieme NQuesto porta alla conclusione che alcuni "infiniti" sono più grandi di altri!
